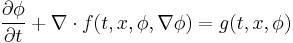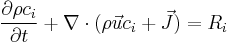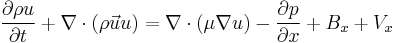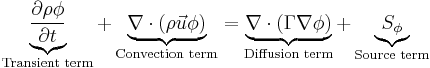Generic scalar transport equation

The generic scalar transport equation is a general partial differential equation that describes transport phenomena such as heat transfer, mass transfer, fluid dynamics (momentum transfer), etc. A general form of the equation is

$\big. \frac{\partial \phi}{\partial t } %2B \nabla \cdot f(t,x,\phi,\nabla\phi) = g(t,x,\phi)$

where $f$ is called the flux, and $g$ is called the source.

All the transfer processes express a certain conservation principle. In this respect, any differential equation addresses a certain quantity as its dependent variable and thus expresses the balance between the phenomena affecting the evolution of this quantity. For example, the temperature of a fluid in a heated pipe is affected by convection due to the solid-fluid interface, and due to the fluid-fluid interaction. Furthermore, temperature is also diffused inside the fluid. For a steady-state problem, with the absence of sources, a differential equation governing the temperature will express a balance between convection and diffusion.

A brief inspection of the equations governing various transport phenomena reveal that all of these equations can be put into a generic form thus allowing a systematic approach for a computer simulation. For example, the conservation equation of a concentration of a substance 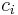$c_i$ is

$\frac{\partial{\rho c_i}}{\partial t } %2B \nabla \cdot (\rho \vec u c_i %2B \vec J) = R_i$

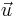where $\vec u$ denotes the velocity field, 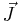$\vec J$ denotes the diffusion flux of the chemical species, and 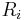$R_i$ denotes the rate of generation of 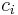$c_i$ caused by chemical reaction.

The x-momentum equation for a Newtonian fluid can be written as

$\frac{\partial{\rho u}}{\partial t} %2B \nabla \cdot (\rho \vec u u ) =\nabla \cdot (\mu \nabla u ) - \frac {\partial p}{\partial x} %2B B_x %2B V_x$

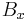where $B_x$ is the body force in the x-direction and 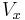$V_x$ includes the viscous terms that are not expressed by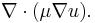 $\nabla \cdot (\mu \nabla u ).$

Upon inspection of the above equations, it can be inferred that all the dependent variables seem to obey a generalized conservation principle. If the dependent variable (scalar or vector) is denoted by $\big. \phi$ , the generic differential equation is^[1]

$\underbrace{ \frac{\partial{\rho \phi}}{\partial t}}_{\text{Transient term}} %2B \underbrace{ \nabla \cdot (\rho \vec u \phi )}_{\text{Convection term}} =\underbrace {\nabla \cdot (\Gamma \nabla \phi )}_{\text{Diffusion term}} %2B \underbrace {S_{\phi}}_{\text{Source term}}$

where $\Gamma$ is the diffusion coefficient, or diffusivity.

The transient term, 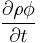$\big. \frac{\partial{\rho \phi}}{\partial t}$ , accounts for the accumulation of $\big. \phi$ in the concerned control volume.
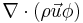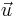The convection term, $\nabla \cdot (\rho \vec u \phi )$ , accounts for the transport of $\big. \phi$ due to the existence of the velocity field (note the velocity $\vec u$ multiplying $\big. \phi$ ).
The diffusion term, 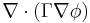$\nabla \cdot (\Gamma \nabla \phi )$ , accounts for the transport of $\big. \phi$ due to its gradients.
The source term, 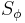$\big. S_{\phi}$ , accounts for any sources or sinks that either create or destroy $\big. \phi$ . Any extra terms that cannot be cast into the convection or diffusion terms are considered as source terms.

The objective of all discretization techniques (finite difference, finite element, finite volume, boundary element, etc.) is to devise a mathematical formulation to transform each of these terms into an algebraic equation. Once applied to all control volumes in a given mesh, we obtain a full linear system of equations that needs to be solved.

1 Scalar transport equation in financial mathematics
2 See also
3 References
4 External links

Scalar transport equation in financial mathematics

Some equations that governs the dynamics of financial derivatives in financial markets can be also categorized as generic scalar transport equations. Examples include the Black-Scholes equation.

References

^ Patankar, S. V. (1980). Numerical Heat Transfer and Fluid Flow. Taylor & Francis. ISBN 978-0891165224.

External links

This article incorporates text from the article Generic_scalar_transport_equation on CFD-Wiki that is under the GFDL license.

Generic scalar transport equation

Contents

Scalar transport equation in financial mathematics

See also

References

External links